Square Tiling Of A Sphere, Part 2/3

In the previous post I described how I learned about HEALPix because I wanted to try covering a sphere with square tiles for a game map. During that exploration I realized that HEALPix with 12 square regions is similar to cubes with 6 square regions, but HEALPix has some nice properties for numerical calculations such as spherical harmonics. I don't need those properties. Instead, I am looking for something that's simpler to program, so I explored cubes.

Earth mapped onto a cube

The goal is the same: I want to play a game on a flat top-down tile map (roguelikes, Dwarf Fortress, Factorio, etc.), but these games have one of three approaches to the map:

1. The map is finite and has borders. You can't move past the border. Most roguelikes fall into this category. SimCity, Dwarf Fortress, and most building games do as well.
2. The map is finite and but some borders allow wrapping. Civilization allows east/west wrapping (cylinder); Asteroid has both east/west and allow north/south wrapping (torus).
3. The map is infinite, so it has no borders. Factorio works this way, with a procedurally generated map.

I wanted to explore type 2, but with a sphere instead of a cylinder or torus. The usual approaches to representing a sphere with flat tiles is to use one of the 5 Platonic solids: tetrahedron, cube, octahedron, dodecahedron, isocahedron. There are also approaches that aren't based on Platonic solids: HEALPix, Mercator-like projections, Peirce Quincucial, and others.

In the previous post I mentioned that this is a "gamejam" style project. I give myself one week to work on the topic, and then I wrap it up. If I found something interesting I'll write it up, but many times I'll discard the project. Allowing myself to discard projects removes the penalty for making a "wrong turn". This allows me to explore more quickly.

After HEALPix I decided to explore cubes for the next week's project, using cube maps from graphics programming. It turned out not to be so useful. I had made a wrong turn. That's ok! Because each of these is a separate standalone tiny project, I can easily abandon the code and move on.

The flat square tile map and also its projection onto a sphere

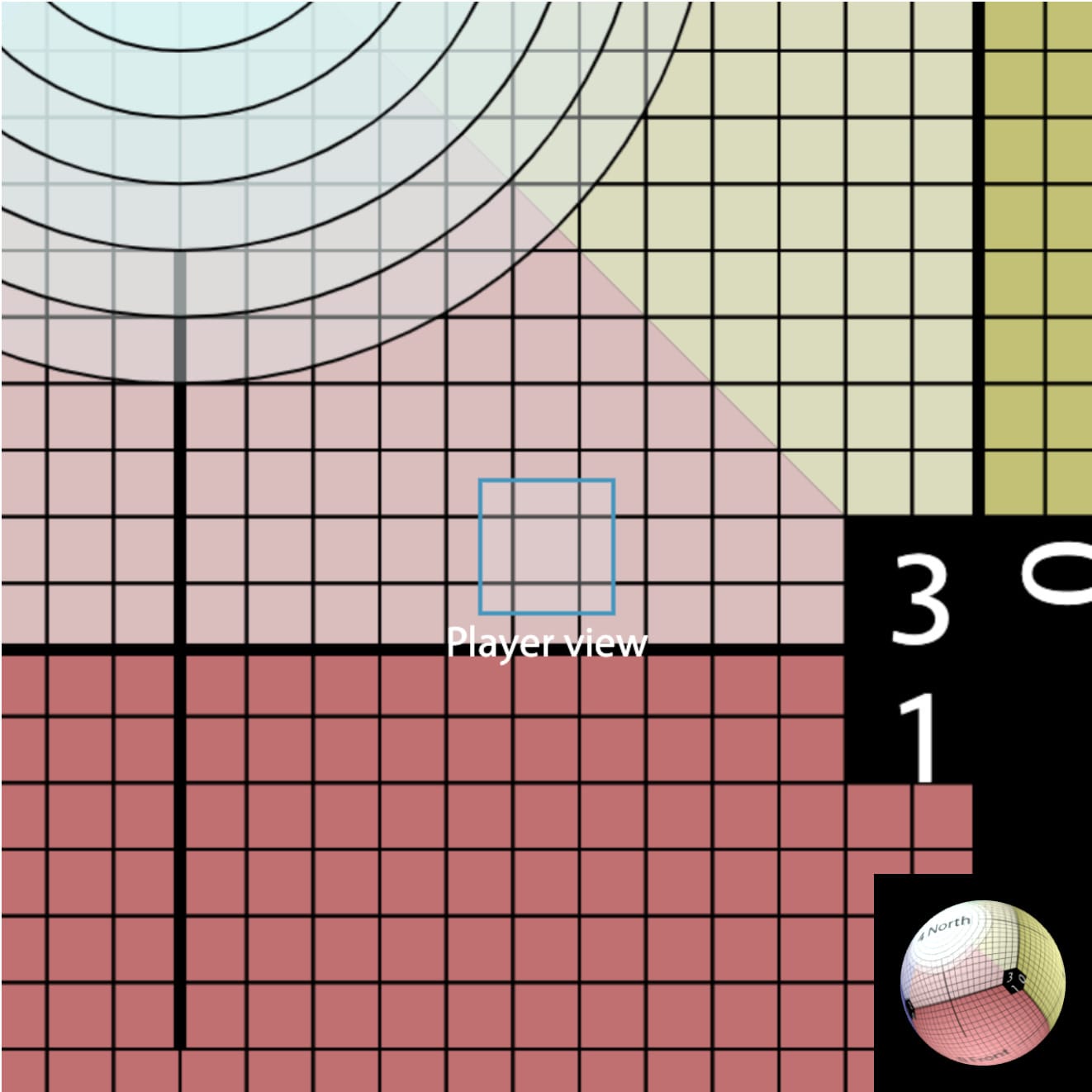
The week after that worked pretty well. I was able to learn how to render and also represent a square grid map on a sphere/cube.

I wrote notes about square tiles on a cube/sphere, including some animations showing how a cube morphs into a sphere, how a cube unfolds onto a plane, and how there are different ways to project a grid on the sphere.

The next "gamejam" style project will be to generate a map on this sphere.